Question

How much longer is CD compared to AB ? Round your solution to 2 decimal points.

Answer 1

CD is 0.66 units longer than AB.

Step-by-step explanation:

Coordinates of A and B are (-11, 4) and (-8, 8)

Therefore, from the formula of distance between two points (x, y) and (x', y')

d =
`\sqrt{(x-x')^(2)+(y-y')^(2)}`

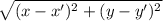
Distance AB =
`\sqrt{(-11+8)^(2)+(4-8)^(2)}`

AB =
`√(9+16)`

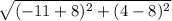
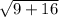
AB = 5

Similarly distance between C (3, 2) and D(7, -2) will be

CD =
`\sqrt{(7-3)^(2)+(-2-2)^(2)}`

CD =
`√(32)`

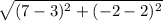
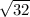
CD = 5.66

Difference between the lengths of AB and CD = 5.66 - 5

= 0.66

Therefore, CD is 0.66 units longer than AB.

Answer 2

• Segment CD is 0.66 units longer than segment AB.

Step-by-step explanation:

Use the distance formula (Pythagoras) between two points to find the length of each segment:

• 
  `length=√((x_2-x_1)^2+(y_2-y_1)^2)`

1) Segment AB:

• Coordinates of point A: (-11,4)
• Coordinates of point B: (-8,8)

• 
  `length=√((-8-(-11))^2+(8-4)^2)=√((3)^2+(4)^2)}=√(9+16)=√(25)=5`

2) Segment CD:

• Coordinates of point C: (3,2)

• Coordinates of point D: (7, -2)

• 
  `length=√((7-3)^2+(-2-2)^2)=√((4)^2+(4)^2)}=√(16+16)=√(32)`

3) Difference:

• 
  `√(32) -5=5.66-5=0.66`