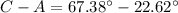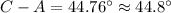Answer:
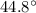
Step-by-step explanation:
We have a right triangle with sides AB, BC=5cm and AC=13cm (the hypotenuse). Let's apply the Pithagorean Theorem to find AB:
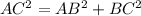 (1)
(1)
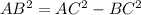 (2)
(2)
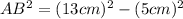 (3)
(3)
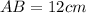 (4)
(4)
Now that we know the value of each side of the triangle, we will use the trigonometric function sine to find the angles C and A (angle B is
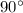 remembering we are talking about a right triangle):
remembering we are talking about a right triangle):
For angle C:
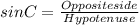
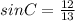 (5)
(5)
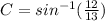 (6)
(6)
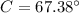 (7)
(7)
For angle A:
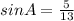 (8)
(8)
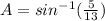 (9)
(9)
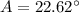 (10)
(10)
Calculating the difference between both angles: