Question

Given the equation 5x2 − 20x + 15 = 0, what are the values of h and k when the equation is written in vertex form a(x − h)2 + k = 0?

h = 2, k = 17
h = 2, k = −5
h = 1, k = 3
h = −1, k = −3

Answer 1

h=2, k=-5

Explanation:

Answer 2

h = 2, k = −5

Explanation:

The given function is
`5x^2-20x+15=0`

We need to complete the square to obtain the function in the form:

`a(x-h)^2+k=0`

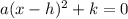
We factor 5 from the first two terms to get:

`5(x^2-4x)+15`

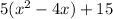
We now add and subtract the square of half the coefficient of x.

`5(x^2-4x+4-4)+15`

`5(x^2-4x+4)-5(4)+15`

`5(x^2-4x+4)-20+15`

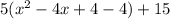
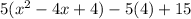
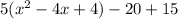
Factor the perfect square expression within the parenthesis:

`5(x-2)^2-5`

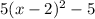
By comparing to
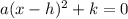`a(x-h)^2+k=0`, we have h=2 and k=-5