Question

A man jogs at a speed of 0.96 m/s. His dog waits 2.3 s and then takes off running at a speed of 3.4 m/s to catch the man. How far will they have each traveled when the dog catches up with the man

Answer 1

When the dog starts running, the man has jogged (0.96 * 2.3 = 2.208) meters.

We can set up an equation to solve for T

2.208 + 0.96T = 3.4T
2.208 = 2.44T
T = 0.904918

You can use either side of the previous equation to evaluate the distance traveled.

2.208 + 0.96 * 0.904918 = 3.076721 meters
3.4 * 0.904918 = 3.076721 meters

Answer 2

The dog and the man meet 3.0767m later.

Explanation:

The first thing to know is the speed formula. It is
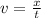`v=(x)/(t)` , where v is speed, x is distance and t is time. If you find x the formula would be
`x=v\cdot t`

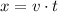
The first step is to obtain the distance equation for the man:

`x_(man)=v_(man)\cdot t=0.96\cdot t`

For the dog's distance equation, a little detail must be taken into account. The dog takes off running 2.3s after the man did. With that in mind, you must subtract 2.3 from t.

`x_(dog)=v_(dog)\cdot (t-2.3)=3.4\cdot (t-2.3)`

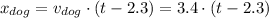
For finding the point where the dog catches up with the man you must match the equations of each one and then obtain find the t value. The procedure is shown:

`x_(man)=x_(dog)`

`0.96\cdot t=3.4\cdot (t-2.3)`

`0.96\cdot t=3.4\cdot t - 7.82`

`2.44\cdot t=7.82`

`t=(7.82)/(2.44)`

`t=3.2049s`

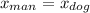
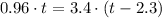
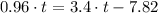
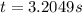
The previous result means that they meet in 3.2049s after the man started running. This value is used in the distance equation of the man.

`x_(man)=0.96\cdot t=(0.96)\cdot (3.2049)`

`x_(man)=3.0767m`

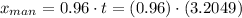
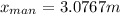
Finally, the dog and the man meet 3.0767m later.