Answer:
a = 3,137
Explanation:
We have to use the sin rule to solve. THis gives ratios of side and opposite side's angle's sin.
Sin rule is:
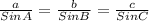
First, we know there are 180 degrees in 3 angles of a triangle, so lets find ∠A:
∠A + ∠B + ∠C = 180
∠A + 11 + 75 = 180
∠A + 86 = 180
∠A = 180 - 86
∠A = 94
Now since we know the angle B and side b pair, we can relate with a and write the sin rule as:
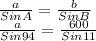
Now we cross multiply and solve for side a:

So last answer choice is right, a = 3137