Answer:
The length of diagonal XU is 6.40 units
Explanation:
* Lets explain how to find the distance between two points
- The rule of the distance between two points

and
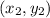 is:
is:

* Lets solve the problem
-From the attached figure:
- The coordinates of the vertex X are (2 , 2)
- The coordinates of the vertex U are (-2 , 7)
∴ The point
 = (2 , 2)
= (2 , 2)
∴ The point
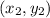 = (-2 , 7)
= (-2 , 7)
∴
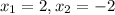
∴
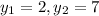
∵

∴
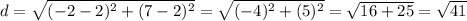
∵

∴ d = 6.40
* The length of diagonal XU is 6.40 units