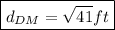Question

112 31415

Tania uses a coordinate plane to map out plans for landscaping a rectangular patio area. On the plan, one
square represents 2 feet. She plans to plant a tree at the midpoint of AC.How far from each comer of the
patio does she plant the tree? Round to the nearest tenth.
AM = MC
ft.; MB = MD =​

Answer 1

Hey there! This problem can be found elsewhere and has been attached below. In order to solve this problem, we have to use the distance formula, but first let's write the given points:

Since one square represents 2 feet, then it is true that:

`A \rightarrow 2(1,2)=(2,4) \ in \ ft \\ \\ B \rightarrow 2(3,2)=(6,4) \ in \ ft \\ \\ C \rightarrow 2(1,-3)=(2,-6) \ in \ ft \\ \\ D \rightarrow 2(3,-3)=(6,-6) \ in \ ft`

We know that Tania plans to plant a tree at the midpoint of AC, so this point can be found by using the Midpoint Formula, let's call this point
`M`, then:

`M=\left((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2)\right) \\ \\ For \ A(x_(1),y_(1)) \ and \ C(x_(2),y_(2)) \\ \\ M=\left((2+2)/(2),(4-6)/(2)\right) \\ \\ M(2,-1)`

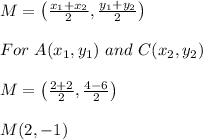
So the distance from each comer of the patio does she plant the tree is:

FROM CORNER A:

`d=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2} \\ \\ A(2,4) \\ M(2,-1) \\ \\ d_(AM)=√((-1-4)^2+(2-2)^2) \\ \\ \boxed{d_(AM)=5ft}`

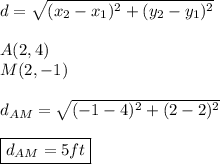
FROM CORNER B:

`B(6,4) \\ M(2,-1) \\ \\ d_(BM)=√((-1-4)^2+(2-6)^2) \\ \\ \boxed{d_(BM)=√(41)ft}`

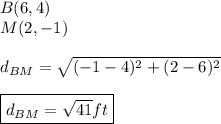
FROM CORNER C:

Same distance as from A:

`\boxed{d_(CM)=5ft}`

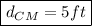
FROM CORNER D:

Same distance as from B:

`\boxed{d_(DM)=√(41)ft}`