Answer:
9 child tickets and 17 adult tickets were sold.
Explanation:
Let the number of adult tickets sold be

and the number of child tickets be
 .
.
The theater sold a total number of 26 tickets.
This means that:
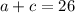 .....eqn1
.....eqn1
The theater made a total sale od $194.
This implies that:
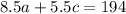 ...eqn2
...eqn2
We make
 the subject in equation 1:
the subject in equation 1:
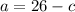 ...eqn3
...eqn3
Substitute equation (3) into equation (2)
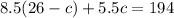
Expand to get:
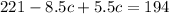
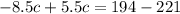
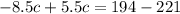
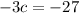
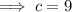
Put c=9 into equation (3) to get:
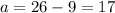
Therefore 9 child tickets and 17 adult tickets were sold.