Question

An object moves along the x axis according to the equation x(t) 3.00t^2 -2.00t 3.00. What is the instantaneous acceleration?

Answer 1

6 m/s^2

Step-by-step explanation:

The object moves along

`x(t)=3t^(2)-2t+3`

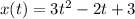
The time rate of change of displacement gives the instantaneous velocity.

It means the differentiation of displacement function with respect to time gives the value of instantaneous velocity.

So, differentiate position function with respect to time, we get

`v = dx/dt`

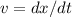
v = 6t - 2

Now we know that time rate of change of velocity gives instantaneous acceleration.

It means the differentiation of velocity function with respect to time gives the value of instantaneous acceleration.

So, differentiate velocity function with respect to time, we get

`a = dv/dt`

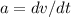
a = 6 m/s^2

Thus, the instantaneous acceleration of the object is 6 m/s^2.