Question

Use the zero product property to find the solutions to the equation (x + 2) (x + 3) = 12.

Answer 1

The answer is 2 fishing method and divide both sides by 6

Answer 2

`x_(1) =-6\\x_(2) =1`

Explanation:

The given equation is

`(x+2)(x+3)=12`

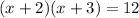
First, we need to apply distributive property to have the quadratic expression

`x^(2) +3x+2x+6=12\\x^(2) +5x+6-12=0\\x^(2) +5x-6=0`

We need to find two numbers which product is -6 and which difference is 5. Those numbers are 6 and 1, because 6 - 1 = 5, and 6(-1) = -6.

`x^(2) +5x-6=(x+6)(x-1)=0`

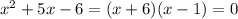
If we apply the zero product property, that means each binomial is equal to zero

`x+6=0\\x-1=0`

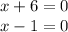
Therefore, the solutions are

`x_(1) =-6\\x_(2) =1`