Question

6a to the 3/4 power
a=16

Answer 1

The answer is 48

Explanation:

* Lets explain how to solve the problem

- The radical can be written as a fraction power:

`\sqrt[n]{x^(m) }=x^{(m)/(n)}`

- We can simplify the fraction power by factorize the base of the power

to numbers divisible by the power if it could

- Ex:
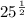`25^{(1)/(2)}` we can factorize 25 to 5² and then

make
`[(5)^(2)]^{(1)/(2)}=(5)^{2*(1)/(2)}=5`

* Lets solve the problem

- We want to find the value of
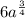`6a^{(3)/(4)}` , where a = 16

- Substitute the value of a by 16

∴
`6(16)^{(3)/(4)}`

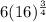
- Lets factorize 16

∵ 16 can be written as 2 × 2 × 2 × 2

∴
`16=2^(4)`

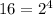
- Replace 16 by
`2^(4)`

∴
`6(2^(4))^{(3)/(4)}=6(2^{4*(3)/(4)})=6(2^(3))`

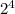
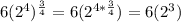
- Now solve 2³

∵ 2³ = 8

∴ 6(8) = 48

∴
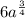`6a^{(3)/(4)}` = 48

* The answer is 48