Question

Tina is saving to buy a notebook computer. She has two options. The first option is to put $500 away initially and save $10 every month. The second option is to put $100 away initially and save $30 every month. After how many months would Tina save the same amount using either option? How much would she save with either option?

Answer 1

Tina would save the same amount using either option after 20 months.

With either option, Tina would save $700.

Explanation:

This problem can be modeled by a first order equation:

Where Tina's saved money after n months is:

S(n) = S(0) + rn, where S(0) is the money put away initially and r is how much she saves every month.

The first option is to put $500 away initially and save $10 every month, so:

`S_(1)(n) = 500 + 10n`

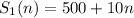
The second option is to put $100 away initially and save $30 every month, so:

`S_(2)(n) = 100 + 30n`

After how many months would Tina save the same amount using either option?

It will happen at the month n in which
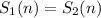`S_(1)(n) = S_(2)(n)`, so:

`S_(1)(n) = S_(2)(n)`

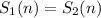
500 + 10n = 100 + 30n

500 - 100 = 30 - 10n

400 = 20n

20n = 400

`n = (400)/(20)`

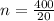
n = 20.

Tina would save the same amount using either option after 20 months.

How much would she save with either option?

We can choose
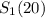`S_(1)(20)` or
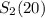`S_(2)(20)`, since they are equal

`S_(1)(20) = 500 + 10(20) = 500 + 200 = 700`

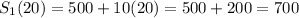
With either option, Tina would save $700.