Question

he function $f$ satisfies\[f(x) + f(2x + y) + 5xy = f(3x - y) + 2x^2 + 1\]for all real numbers $x$, $y$. Determine the value of $f(10)$.

Answer 1

We have f(10) = -49.

Step-by-step explanation:

We have

`f(x)+f(2x+y)+5xy=f(3x-y)+2x^(2)+1`

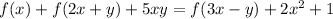
Putting x = 0 and y = 0 we get,

`f(0)+f(0)+0=f(0)+0+1\\\\\therefore f(0)=1`

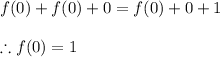
Now put x = 0 in the function equation we get

`f(0)+f(y)+0=f(-y)+1\\\\1+f(y)=f(-y)+1(\because f(0)=1)\\\\\Rightarrow f(-y)=f(y)`

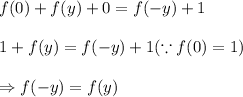
Hence the given function is an even function

Now put x = 2y in the functional equation we get

`f(2y)+f(5y)+10y^(2)=f(5y)+8y^(2)+1\\\\f(2y)=-2y^(2)+1\\\\`

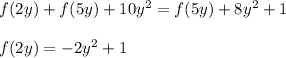
Now put y = x/2 we get

`f(x)=-2((x^(2))/(4))+1\\\\f(x)=(-x^(2))/(2)+1`

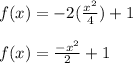
Thus f(10) equals

`f(10)=(-100)/(2)+1`

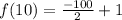
thus f(10) = -49