Determine whether the three given points are collinear. (3, 2), (4, 6), (0, 8) True: they are collinear False: they are not collinear

Question

asked Jul 9, 2020 169k views

2 Answers

AkaBase · Answer 1 · 2020-07-14T11:25:54+0000

Answer:

They are not co-linear.

Explanation:

For three point's to be co linear the slopes of the lines connecting them should be same

Mathematically we can write for
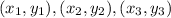
(x_(1),y_(1)),(x_(2),y_(2)),(x_(3),y_(3))

to be co-linear we should have

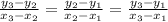
(y_(3)-y_(2))/(x_(3)-x_(2))=(y_(2)-y_(1))/(x_(2)-x_(1))=(y_(3)-y_(1))/(x_(3)-x_(1))

Applying the given values we obtain

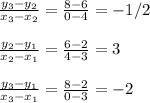
$(y_(3)-y_(2))/(x_(3)-x_(2))=(8-6)/(0-4)=-1/2\\\\(y_(2)-y_(1))/(x_(2)-x_(1))=(6-2)/(4-3)=3\\\\(y_(3)-y_(1))/(x_(3)-x_(1))=(8-2)/(0-3)=-2$

As we can see the values are not equal thus the points are not co-linear.