Question

A student throws a set of keys vertically upward to his fraternity brother, who is in a window a distance h above. The brother's outstretched hands catches the keys on their way up at a time t later. (a) With what initial velocity were the keys thrown? (b) What was the velocity of the keys just before they were caught? (Answer should be in terms of h, t, and g.)

Answer 1

1) The initial velocity equals
`u=(h)/(t)+(gt)/(2)`

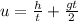
2) The velocity with which the keys were caught equals
`v=(h)/(t)-(gt)/(2)`

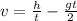
Step-by-step explanation:

Let the keys be thrown with a speed 'u' vertically upwards. Since the keys are caught after time 't' while covering a distance 'h' we can use second equation of kinematics to relate these terms.

According to second equation of kinematics the displacement of an object in 't' time is given by

`\Delta y=ut+(1)/(2)at^(2)`

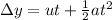
Applying the corresponding values and solving for the initial speed 'u' we get

`h=ut-(1)/(2)gt^(2)\\\\2h+gt^(2)=2ut\\\\\therefore u=(h)/(t)+(gt)/(2)`

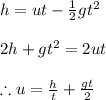
The change in velocities while covering a distance 's' can be found from first equation of kinematics

Thus we have

`v=u+at`

Applying corresponding values we get

`v=u-gt\\\\v=(h)/(t)+(gt)/(2)-gt\\\\=(h)/(t)-(gt)/(2)`