Question

The amount of money Chaz earned for walking dogs is given in the table. Can the relationship be described by a constant rate? Explain.

Answer 1

Yes, the relationship can be described by a constant rate of $18.75 per dog

Explanation:

see the attached figure to better understand the problem

Let

x ----> the number of dogs

y ---> the amount of money earned

we have the points

`(6,112,50), (8,150), (11,206.25)`

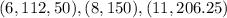
step 1

Find the slope with the first and second point

`(6,112,50), (8,150)`

`m=(150-112.50)/(8-6)=18.75`

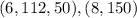
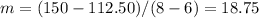
step 2

Find the slope with the first and third point

`(6,112,50), (11,206.25)`

`m=(206.25-112.50)/(11-6)=18.75`

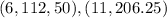
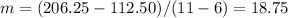
Compare the slopes

The slopes are the same

That means, that the three points lies on the same line

therefore

Yes, the relationship can be described by a constant rate of $18.75 per dog