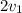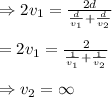Answer:
Given condition is not physically possible. Speed of second lap should be infinite.
Explanation:
Let the speed at which we run the second lap be
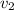
Now by definition of average speed we have
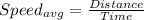
Let the first lap take a time
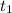 and second lap take a time
and second lap take a time
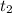
Thus applying the given conditions in the above equation we have
Total distance covered in 2 laps equals 2d
Thus we have
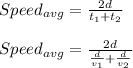
Thus according to the given condition average speed should be