Question

Suppose that the inverse demand for San Francisco cable car rides is pequals20minusStartFraction Upper Q Over 1000 EndFraction ​, where p is the price per ride and Q is the number of rides per day. Suppose the objective of San​ Francisco's Municipal Authority​ (the cable car​ operator) is to maximize its revenues LOADING.... What is the​ revenue-maximizing price? The​ revenue-maximizing price is

Answer 1

Answer: The​ revenue-maximizing price is $10.

Step-by-step explanation:

Given that,

Inverse demand function: P =
`20 - (Q)/(1,000)`

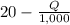
Where,

P - Price per ride

Q - Number of rides per day

Revenue(R) = P × Q

=
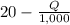`20 - (Q)/(1,000)` × Q

=
`20Q - (Q^(2) )/(1,000)`

Differentiating 'R' with respect to Q for calculating Marginal revenue(MR):

MR =
`20 - (Q)/(500)`

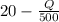
Here, MC = 0

MR = MC

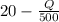`20 - (Q)/(500)` = 0

Therefore, Q = 10,000

P =
`20 - (Q)/(1,000)`

=
`20 - (10,000)/(1,000)`

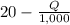
= $10

Hence, the​ revenue-maximizing price is $10.