Question

There are seven empty seats in a theater, and four customers need to find places to sit. How many different ways can these four seat themselves g

Answer 1

Answer: 840

Explanation:

Given : The total number of empty seats in the theater = 7

The number of customers need to find places to sit = 4

Since here order of their sitting matters , then we use permutation to find the number of ways of sitting.

The number of permutations of n things taking r at a time is given by :-

`^nP_r=(n!)/((n-r)!)`

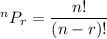
Then , the number of permutations of 7 things taking at a time is given by :-

`^7P_4=(7!)/((7-4)!)\\\\=(7*6*5*4*3!)/(3!)=840`

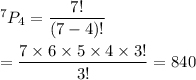
Hence, the number of different ways can these four seat themselves = 840