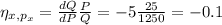Question

Always Round Tire finds that their demand curve is P = 50 − .02 Q. What price and quantity combination will maximize the firm's revenue? What are the total revenue and price elasticity at this point?

Answer 1

Price is 25

Quantity is 1,250

Total revenue= 31,250

Elasticity at that point = -0.1

Step-by-step explanation:

Total revenue (TR) is given by TR=Price x Quantity . We can get the price from the demand equation. Then

`TR=P * Q= (50-0.2Q)*Q=50Q * 0.2Q^2`

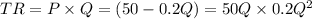
where Q is the quantity and P is the price. To find the maximum revenue we take derivatives with respect to the quantity and equalize it to zero

`(d)/(dQ)TR=50-0.04Q=0`

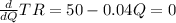
solving for Q we have that Q=1,250 replacing in the demand curve we can get the price
`P=50-0.02Q=50-0.02* 1250=25`

Total revenue is
`1250*25=31,250`

Elasticity at this point is
`\eta_(x,p_x)=(dQ)/(dP)(P)/(Q)=-5(25)/(1250)=-0.1`