Question

A right triangle has one angle that measure 23o. The adjacent leg measures 27.6 cm and the hypotenuse measures 30 cm. What is the approximate area of the triangle? Round to the nearest tenth. Area of a triangle = bh 68.7 cm2 161.8 cm2 381.3 cm2 450.0 cm2

Answer 1

To work out the area of a triangle, you can use the following equation:

`Area = (1)/(2) absin(c)`

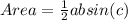
a and b are are adjacent legs of the triangle, and c is the angle inbetween the two legs (a and b).

We know that:

a = 27.6

b = 30

c = 23°

So to get our answer, we just substitute in the values into the equation:

`Area = (1)/(2) absin(c)`

`Area = (1)/(2) (27.6)(30)(sin(23))`

`Area = 161.76`

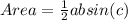
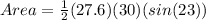
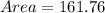
161.76 rounds up to 161.8

_______________________________

Answer:

161.8 cm²

Answer 2

`A=161.8\ cm^2`

Explanation:

we know that

The area of triangle applying the law of sines is equal to

`A=(1)/(2)(a)(c)sin(B)`

where

a is the adjacent side to the angle

c is the hypotenuse

B is the angle between the two given sides ( adjacent leg and hypotenuse)

we have

`a=27.6\ cm`

`c=30\ cm`

`B=23\°`

substitute

`A=(1)/(2)(27.6)(30)sin(23\°)`

`A=161.8\ cm^2`