Question

Find an equation of the line passing through the point A(4,7) and perpendicular to the line through points B(-1,-2) and C(5,8).

Answer 1

The equation of line is
`y=-0.6x+9.4`

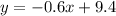
Explanation:

Since the line is perpendicular to the line passing through (-1,-2) and (5,8) the product of it's slope and the line is related as

`m_(1)* m_(2)=-1`

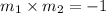
Slope of line through (-1,-2) and (5,8) is

`m_(2)=(y_(2)-y_(1))/(x_(2)-x_(1))=(8-(-2))/(5-(-1))\\\\\therefore m_(2)=(10)/(6)\\\\Now,\\\\m_(1)* m_(2)=-1\\\\\therefore m_(1)=(-1)/((10)/(6))=(-6)/(10)=-0.6`

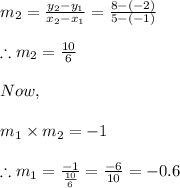
Now we know that general equation of line is given by

`y=m_(1)x+c`

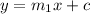
Applying value we get

`y=-0.6x+c`

The value of 'c' can be obtained as we know that the line is passing through (4,7)

Thus we have

`7=-0.6* 4+c\\\\\therefore c=9.4\\\\\therefore y=-0.6x+9.4`