Question

Determine the length of the leg of a 45o – 45o – 90o triangle with a hypotenuse length of 15 inches. ( ANSWER NEEDS TO BE IN REDUCED RADICAL FORM )

Answer 1

The lenghts of both legs:
`(15√(2))/(2)\ inches`

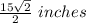
Explanation:

By definition, when a triangle has angles that measures 45°, 45° and 90°, its legs are congruent.

Then, knowing the lenght of the hypotenuse, we can find the lenght (in inches) of any leg of the given triangle by applying the Trigonometric Identity
`sin\alpha=(opposite)/(hypotenuse)`:

`sin(45\°)=(leg)/(15)\\\\leg=(15)/(√(2))`

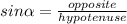Finally, simplifying, we get:

`leg=(15(√(2)))/((√(2))(√(2)))=(15√(2))/(2)`