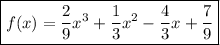Question

Find a cubic function f(x) = ax3 + bx2 + cx + d that has a local maximum value of 3 at x = −2 and a local minimum value of 0 at x = 1. f(x) =

Answer 1

The graph of
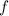`f` passes through the points (-2, 3) and (1, 0), so

`f(-2)=3 \implies -8a + 4b - 2c + d = 3`

`f(1) = 0 \implies a + b + c + d = 0`

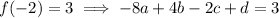
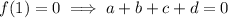
Since these are the sites of local extrema, we know that
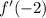`f'(-2)` and
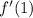`f'(1)` are either zero or undefined.
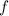`f` is a polynomial, so it's continuous and differentiable everywhere, so only the zero-case is relevant.

We have derivative

`f'(x) = 3ax^2 + 2bx + c`

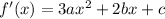
and so

`f'(-2) = 0 \implies 12a - 4b + c = 0`

`f'(1) = 0 \implies 3a + 2b + c = 0`

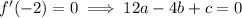
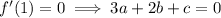
Solve for
`a,b,c,d`.

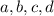• In the first two equations, we can eliminate
`d`.

`(-8a+4b-2c+d) - (a+b+c+d) = 3-0 \implies -9a + 3b - 3c = 3`

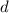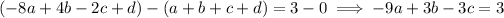
• Now eliminate
`c` by combining any two equations in
`a,b,c`.

`(12a-4b+c) - (3a+2b+c) = 0-0 \implies 9a-6b = 0 \implies 3a-2b=0`

`3(3a+2b+c) + (-9a+3b-3c) = 3(0)+3 \implies 9b = 3`

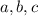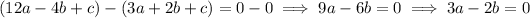
Then we have

`9b = 3 \implies b = \frac13`

`3a-2b=0 \implies 3a = \frac23 \implies a=\frac29`

`3a+2b+c=0 \implies c = -\frac43`

`a+b+c+d=0 \implies d = \frac79`

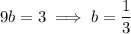
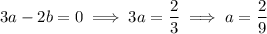
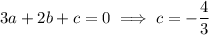
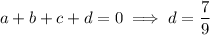
and so the cubic function is

`\boxed{f(x) = \frac29 x^3 + \frac13 x^2 - \frac43 x + \frac79}`

Answer 2

Explanation:

f(-2)=3

f(1) =0

f'(-2)=0

f' (1) = 0 ..... continue