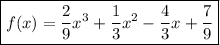The graph of
 passes through the points (-2, 3) and (1, 0), so
passes through the points (-2, 3) and (1, 0), so
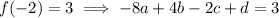
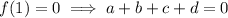
Since these are the sites of local extrema, we know that
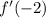 and
and
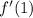 are either zero or undefined.
are either zero or undefined.
 is a polynomial, so it's continuous and differentiable everywhere, so only the zero-case is relevant.
is a polynomial, so it's continuous and differentiable everywhere, so only the zero-case is relevant.
We have derivative
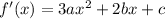
and so
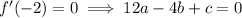
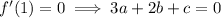
Solve for
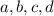 .
.
• In the first two equations, we can eliminate
 .
.
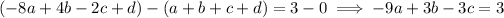
• Now eliminate
 by combining any two equations in
by combining any two equations in
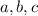 .
.
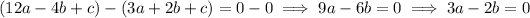

Then we have
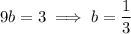
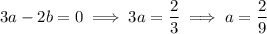
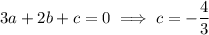
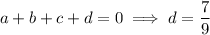
and so the cubic function is