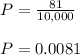Question

A locker combination contains four digits. Each digit can be from 0 through 9. What is the probability that a 4-digit combination chosen at random is made up of 4 digits that are all greater than 6 if each digit can be repeated?

1. Find the total number of possible outcomes.
1. (10)(10)(10)(10)
2. Find the number of favorable outcomes.
2. (3)(3)(3)(3)
3. Use the formula
3.
P (event) = Number of favorable outcomes
Number of possible outcomes

Answer 1

Answer: 81/10,000

Explanation:

Just did it

Answer 2

`P=0.0081`

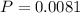
Explanation:

We know that the probability of an event is:

`P (event) = (Number\ of\ favorable\ outcomes)/(Number\ of\ possible\ outcomes)`

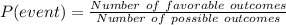
Note that between 0 and 9 there are 10 possible digits {0,1,2,3,4,5,6,7,8,9}

If each digit can be repeated and the combination has 4 digits then the number of possible combinations S is:

`S = 10 * 10 * 10 * 10 = 10 ^ 4 = 10,000`

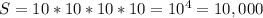
If all digits obtained must be greater than six, then the possible digits that can be obtained are three: {7,8,9}.

If the combination is 4 digits then the number of results that can be obtained are:

`S = 3 * 3 * 3 * 3 = 3 ^ 4 = 81`

So:

Number of favorable outcomes = 81

Number of possible outcomes = 10,000

Finally the probability is:

`P = (81)/(10,000)\\\\P=0.0081`