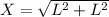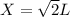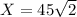Question

Find the value of x. ( ANSWER NEEDS TO BE IN REDUCED RADICAL FORM )

Answer 1

`X = 45√(2)`

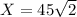
Explanation:

All sides are of equal length.

`L = 45`

So the figure is a square.

To find the x side, which is the hypotenuse of the triangle, we use Pythagoras' theorem:

`X = √(L ^ 2 + S ^ 2)`

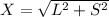
Where

S is the length of the adjacent side and L is the length of the opposite side and X is the hypotenuse.

Since S and L are sides of a square, it is true that:

`S = L = 45`

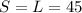
So:

`X = √(L ^ 2 + L ^ 2)`

`X = √(2L ^ 2)`

`X = √(2)L`

`X = 45√(2)`