Check the forward differences of the sequence:
22 - 8 = 14
50 - 22 = 28 = 2*14
106 - 50 = 56 = 4*14
218 - 106 = 112 = 8*14
442 - 218 = 224 = 16*14
The differences are the products of increasing powers of 2 and 14:

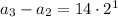
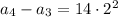
and so on, with
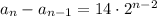
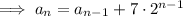
Then the sequence has the recursive definition,
