Answer:
1) Option 2 - x=-3 or x=5
2) option 4 - x=4 or x=7
3) Option 3 - x=-4 or x=9
4) Option 1 - x=4 or x=-6
5) Option 1 -
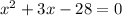
Explanation:
1) Solve using the zero product property
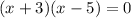
Solution :
Zero product property states that if ab=0 then a=0 or b=0.
Applying,
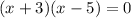
Either
 or
or
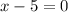
Either
 or
or

So, Option 2 is correct.
2) Solve by factoring and applying the zero product property
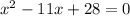
Solution :
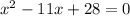
Applying middle term split,
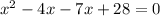

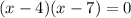
Applying zero product property,
Either
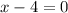 or
or

Either
 or
or
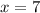
So, Option 4 is correct.
3) Solve by factoring and applying the zero product property

Solution :

Applying middle term split,
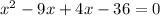
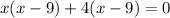
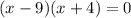
Applying zero product property,
Either
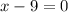 or
or
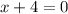
Either
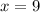 or
or
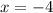
So, Option 3 is correct.
4) For what values is the following true?
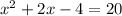
Solution : To get the result we factor the equation,
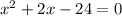
Applying middle term split,
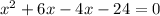
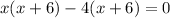

Applying zero product property,
Either
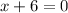 or
or
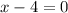
Either
 or
or

So, Option 1 is correct.
5) To find the solution to the equation using factoring, we need to first write it in standard form. Which of the following choices is equivalent to the equation :
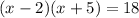
Solution :
To write in standard form we just multiply the terms,
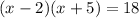
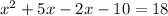
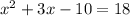
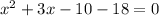
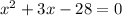
So, Option 1 is correct.