Answer:
18.03 cubic feet
Explanation:
Hello,
Step 1
find the volume of the sphere when radius= 5 ft

Step 2
find the volume of the sphere when radius= 5.1 ft
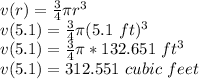
Step 3
Compare the Volumes to find the change
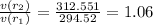
the volumen of the sphere with radius = 5.1 is 1.06 times bigger than the first one(r=5)
Now, find the change
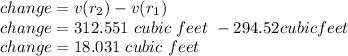
change=18.03 cubic feet
Have a great day.