Question

The first ionization energy, ????, of a carbon atom is 1.81 aJ. What is the wavelength of light, in nanometers, that is just sufficient to ionize a carbon atom?

Answer 1

109.8 nm

Step-by-step explanation:

The first ionization energy of a hydrogen atom is,

`E=1.81aJ\\E=1.81* 10^(-18) J`

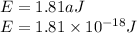
And Plank's constant,
`h=6.626* 10^(-34)Js`

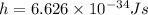
And the speed is,
`c=3* 10^(8)m/s`

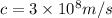
Now the formula for energy will be,

`E=(hc)/(\lambda)`

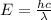
Put all the variable after rearranging for lambda.

`\lambda=(6.626* 10^(-34)Js(3* 10^(8)m/s))/(1.81* 10^(-18) J) \\\lambda=10.98*10^(-8)m\\\lambda=109.8* 10^(-9)m\\\lambda=109.8 nm`

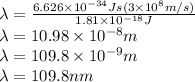
Therefore the wavelength of light is 109.8 nm to ionize a carbon atom .