Answer:

Explanation:
The general equation for a circle is:

where
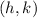 is the center of the circle, and
is the center of the circle, and
 is the radius.
is the radius.
The equation we have is:
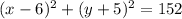
we can also write this as follows:

this way we can see that
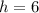
and
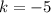
so, since the center of the circle is at
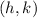
substituting the values:
 this are the coordinates of the center of the circle
this are the coordinates of the center of the circle