Question

How many words of five letters can be created that start with the letter T, contain 2 other consonats and end with 2 vowels? Note that a word is any combination of 5 letters but letters cannot be repeated.

Answer 1

If we're only counting 5 vowels (A, E, I, O, U) and 20 consonants (everything else, minus T), then there are

`\dbinom52=(5!)/(2!(5-2)!)=10`

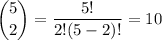
ways of picking the vowels, and

`\dbinom{20}2=(20!)/(2!(20-2)!)=190`

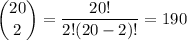
ways of picking the consonants.

We want the word to start with T, and we'll allow any arrangement of the other 4 letters, so that the total number of words is

`4!\dbinom52\dbinom{20}2=\boxed{45,600}`

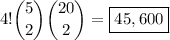
Keep in mind that this means words like TRIES and TIRES are treated as different.