Answer:
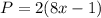
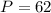 at
at

Explanation:
Given: The length of the rectangle is
 and width of the rectangle is
and width of the rectangle is
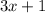
To find: An expression that can be used to find the perimeter of the rectangle, and the perimeter when x is 4.
Solution:
Here, Length is given as

width of the rectangle is
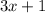
Let P represents the perimeter of the rectangle
We know that perimeter of a rectangle is
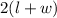
So, we have
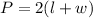
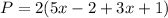
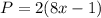
Therefore, the expression to find the perimeter is
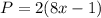
Now, we need to find the perimeter at

On substituting
 in
in
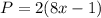 we have,
we have,
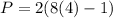
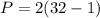

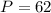
Hence, the perimeter is 62 units when x is 4.