The length of the radius of the circle is 8 units
How to determine the length of the radius of the circle?
From the question, we have the following parameters that can be used in our computation:
The circle
Where, we have
ADB = 8π
The length of an arc is calculated using
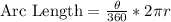
In this case, we have
θ = 180 --- angle in a semicircle
So, we have
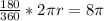
This gives
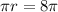
Divide
r = 8
Hence, the length of the radius of the circle is 8 units
Question
In the circle to the left, segment AB is a diameter. If the length of arc ADB is 8π, what is the length of the radius of the circle?