Question

Does the following system have a unique solution? Why?

A) No, because the determinant of the coefficient matrix is 0.


B) No, because the determinant of the coefficient matrix is 12.


C) Yes, because the determinant of the coefficient matrix is 0.


D) Yes, because the determinant of the coefficient matrix is 12.

Answer 1

A) No, because the determinant of the coefficient matrix is 0.

Explanation:

`\begin{cases}2x - 3y = 5\\-4x + 6y = -4\end{cases}\\x = (D_(x))/(D)\\\\y = (D_(y))/(D)\\\\D = \begin{vmatrix}2 & -3 \\-4 & 6 \end{vmatrix}\\\\D= 2*6-(-4)(-3)= 12 - 12 = \mathbf{0}\\\text{The system of equations has no solution because}\\\boxed{\textbf{the determinant of the coefficient matrix is zero}}`

Answer 2

A) No, because the determinant of the coefficient matrix is 0.

Explanation:

The determinant of the matrix
`\left[\begin{array}{cc}a&b\\c&d\end{array}\right]` is
`ad-bc`.

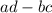The given system is
`\left \{ {{2x-3y=5} \atop {-4x+6y=-4}} \right.`.

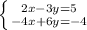The coefficient matrix for this system is:
`\left[\begin{array}{cc}2&3\\-4&6\end{array}\right]`

The determinant of this matrix is
`6*2--3*-4=12-12=0`

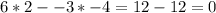
Since the determinant is zero, the system has no unique solution.

The correct choice is A.