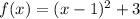Question

Which function in vertex form is equivalent to f(x) = 4 + x2 – 2x? f(x) = (x – 1)2 + 3 f(x) = (x – 1)2 + 5 f(x) = (x + 1)2 + 3 f(x) = (x + 1)2 + 5

Answer 1

Answer: First Option

`f (x) = (x-1) ^ 2 + 3`

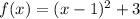
Explanation:

Quadratic quadratic functions have the following form:

`f (x) = (x-h) ^ 2 + k`

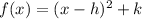
Where the point (h, k) is the vertex of the function.

For a quadratic function of the form
`f (x) = ax ^ 2 + bx + c` the vertex of the function is at the point
`(-(b)/(2a), f((-b)/(2a)))`

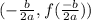
In this case the function is:
`f(x) = 4 + x^2 - 2x\\\\f(x)=x^2 -2x +4`

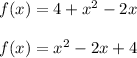
Then:

`a=1\\b=-2\\c=4`

The vertex is:

`(-((-2))/(2(1)), f((2)/(2(1))))`

`(1, f(1))`

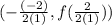
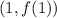
Note that

`f(1) = (1)^2 -2(1) +4\\\\f(1)=1-2+4=3`

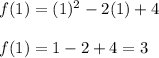
Therefore the vertex is the point
`(1, 3)`

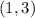
Finally we have that
`h=1,\ k=3`

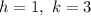
The function in vertex form is :

`f (x) = (x-1) ^ 2 + 3`