Question

Which is one of the transformation applied to the graph of f(x)=x2 to produce the graph of g(x)=2x2-28x+3?

Answer 1

The graph of f(x) stretch vertically by factor 2, shifts 7 units right and 95 units down to get the graph of g(x).

Explanation:

The given functions are

`f(x)=x^2`

`g(x)=2x^2-28x+3`

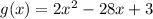
Rewrite the function g(x) in vertex form.

`g(x)=2(x^2-14x)+3`

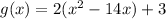
If an expression is defined as
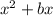`x^2+bx` then we need to add
`((b)/(2))^2` to make it perfect square.

In the above parenthesis b=-14. So add 7² in the parenthesis.

`g(x)=2(x^2-14x+7^2-7^2)+3`

`g(x)=2(x^2-14x+7^2)-2(7^2)+3`

`g(x)=2(x-7)^2-2(49)+3`

`g(x)=2(x-7)^2-98+3`

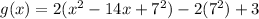
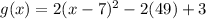
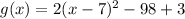
`g(x)=2(x-7)^2-95` .... (1)

The translation is defined as

`g(x)=kf(x+a)^2+b` .... (2)

Where, k is stretch factor, a is horizontal shift and b is vertical shift.

If 0<k<1, then the graph compressed vertically by factor k and if k>1, then the graph stretch vertically by factor k.

If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.

If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.

On comparing (1) and (2), we get

`k=2,a=-7,b=-95`

It means the graph of f(x) stretch vertically by factor 2, shifts 7 units right and 95 units down to get the graph of g(x).

Answer 2

f(x) shifted right 7 units

Explanation:

vertex form of g(x) is g(x) = 2(x – 7)2 – 95

First of all we have to remember the translations rule:

f(x)+b shifts the function b units upward

f(x)-b shifts the function b units downwards.

f(x+b) shifts the function b units to the left

f(x-b) shifts the function b units to the right

From the vertex form 2(x – 7)2 – 95 we can conclude that the parent function f(x) has been shifted 7 units to the right and 91 units upward.

So we can say that f(x) shifted right 7 units....