Question

Liz wants to estimate the percentage of people who rent their home. She surveys 320 individuals and finds that 176 rent their home. Find the margin of error for the confidence interval for the population proportion with a 98% confidence level.

Answer 1

Answer: 0.065

Explanation:

Given : Sample size : n= 320

The sample proportion of people who rent their home :
`p=(176)/(320)=0.55`

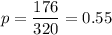
Significance level :
`\alpha:1-0.98=0.02`

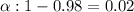
Then , Critical value :
`z_(\alpha/2)=2.33`

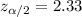
The formula to find the margin of error : -

`E=z_(\alpha/2)\sqrt{(p(1-p))/(n)}\\\\\Rightarrow\ E=(2.33)\sqrt{(0.55(1-0.55))/(320)}\\\\\Rightarrow\ E=0.064799034281\approx0.065`

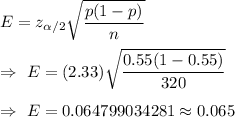
Hence, the margin of error for the confidence interval for the population proportion with a 98% confidence level =0.065