Question

You plan to invest in bonds that pay 6.0%, compounded annually. If you invest $10,000 today, how many years will it take for your investment to grow to $25,000?

Answer 1

The answer is 16 years.

Step-by-step explanation:

The formula for calculating the value of an investment that is compounded annually is given by:

`V(n)=(1+R)^nP`

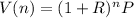
Where:

`n` is the number of years the investment is compounded,

`R` is the annual interest rate,

`P` is the principal investment.

We know the following:

`25000=(1+0.06)^n * 10000`

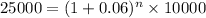
And we want to clear the value n from the equation.

The problem can be resolved as follows.

First step: divide each member of the equation by
`10,000`:

`( 25000)/(10000)=(1+0.06)^n * ( 10000)/(10000)`

`2.5=(1.06)^n`

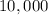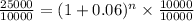
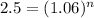
Second step: apply logarithms to both members of the equation:

`log(2.5)=log (1.06)^n`

Third step: apply the logarithmic property
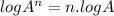`logA^n=n.logA` in the second member of the equation:

`log(2.5)=n.log (1.06)`

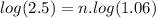
Fourth step: divide both members of the equation by
`log1.06`

`(log(2.50))/(log (1.06)) =n`

`n= 15.7252`

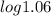
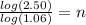
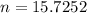
We can round up the number and conclude that it will take 16 years for $10,000 invested today in bonds that pay 6% interest compounded annually, to grow to $25,000.