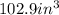Answer:
Explanation:
In order to calculate the space between the sphere and the cube we need to calculate the volume of the cube and then the volume of the sphere. I have attached an illustration below to help you better understand the situation.

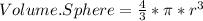 .... r is radius which is half of diameter.
.... r is radius which is half of diameter.
Now that we know the formulas we can solve for the volumes.
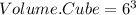
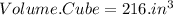
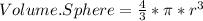
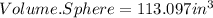
Now we can subtract the volume of the sphere from the volume of the cube in order to calculate the space between them
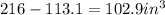
The space between is that of