Question

It takes 3.0 eV of energy to excite an electron in a 1-dimensional infinite well from the ground state to the first excited state. What is the width L of the box?

Answer 1

0.614 nm

Step-by-step explanation:

Energy of the nth state of one dimensional infinite wall is,

`E=(n^(2) h^(2) )/(8mL^(2) )`

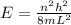
Given the energy to excite an electron from ground state to first excited state is,

`\Delta E=3eV\\\Delta E=3(1.6*10^(-19))J`

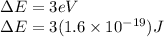
And the Plank's constant is,
`h=6.626*10^(-34)Js`

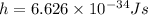
Mass of electron,
`m=9.1*10^(-31)kg`

Now the energy will of a 1 dimensional infinite wall which excite an electron from ground state to first excited state will be,

`\Delta E=(2^(2) h^(2) )/(8mL^(2) ) -(1^(2) h^(2) )/(8mL^(2) )`

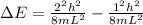
Put all the variables in above equation and rearrange it for L.

`L^(2) =(3((6.626*10^(-34)Js)^(2) ))/(8*9.1*10^(-31)kg*3(1.6*10^(-19))J) \\L^(2) =0.376922012*10^(-18) m^(2)\\ L=0.6139*10^(-9)m\\ L=0.614nm`

Therefore the width of the box is 0.614 nm.