Question

n a survey of 1227 ​people, 828 people said they voted in a recent presidential election. Voting records show that 65​% of eligible voters actually did vote. Given that 65​% of eligible voters actually did​ vote.A) Find the probability that among 1227 randomly selected​ voters, at least 828 actually did vote.B) What do the results from part​ (a) suggest?

Answer 1

Answer: 0.0344

Explanation:

For binomial distribution :-

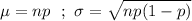`\mu=np\ \ ;\ \sigma=√(np(1-p))`, where p is the proportion of success in each trial and n is the sample size.

Given : Sample size : n=1227

The proportion of people said they voted in a recent presidential election :p=0.95

Then,
`\mu=1227(0.65)=797.55\ \ ;\ \sigma=√((1227)(0.65)(0.35))=16.71`

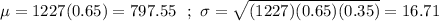
Let X be the binomial variable.

z-score :
`z=(x-\mu)/(\sigma)`

For x= 828

`z=(828-797.55)/(16.71)=1.82`

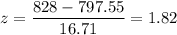
Then, probability that among 1227 randomly selected​ voters, at least 828 actually did vote is given by :-

`P(x\geq828)=P(z\geq1.82)=1-P(z<1.82)-P(z<-3.91)\\\\=1-0.9656205=0.0343795\approx0.0344`

Hence, the probability that among 1227 randomly selected​ voters, at least 828 actually did vote= 0.0344