Answer:
Explanation:
Let x be the wait times before a call is answered in phone calls.
The claim is x bar <3.3 minutes
Sample size n =62
Sample mean - x bar = 3.24 minutes
Population std dev =
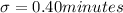
Since population std dev is known and also sample size is sufficiently large, we can use Z test.
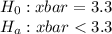
(one tailed test)
Mean difference = 3.24-3.3 = -0.06 min
Std error of sample =
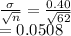
Z = tset statistic =
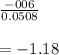
p value = 0.119
Since p value > alpha, we accept null hypothesis.
There is no evidence to support the claim at alpha = 0.08