1. Divide all terms by a:
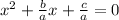
2. Subtract the constant (which is c/a):
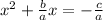
3. Complete the square, then add the constant to both sides:
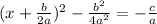 (now add the constant in terms of a and b)
(now add the constant in terms of a and b)
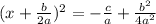 (now simplify the fractions on the right side)
(now simplify the fractions on the right side)
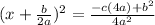
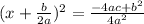 (now just put the b^2 in front)
(now just put the b^2 in front)
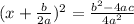
4. Square root both sides and simplify the right side:
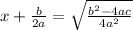 (you can square root the bottom bit of the fraction fully)
(you can square root the bottom bit of the fraction fully)

5. Now just solve for x:
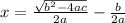 (now simplify)
(now simplify)
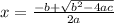 (note: it should be a plus or minus sign infront of the squareroot, not just a plus sign -it's just that i can't write it in )
(note: it should be a plus or minus sign infront of the squareroot, not just a plus sign -it's just that i can't write it in )
_____________________________
If you have any questions, feel free to ask.