Answer:
1.
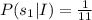
2.
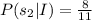
3.
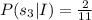
Explanation:
Given information:
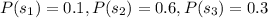
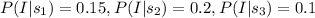
(1)
We need to find the value of P(s₁|I).
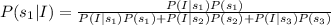
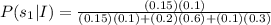
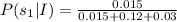
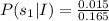
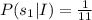
Therefore the value of P(s₁|I) is
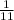 .
.
(2)
We need to find the value of P(s₂|I).
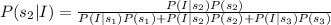
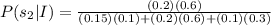
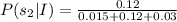
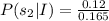
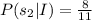
Therefore the value of P(s₂|I) is
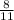 .
.
(3)
We need to find the value of P(s₃|I).
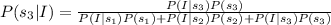
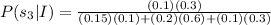
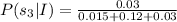
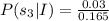
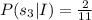
Therefore the value of P(s₃|I) is
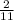 .
.