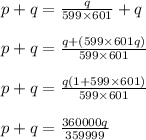Question

Let p = the product of all the odd integers between 500 and 598, and let q = the product of all the odd integers between 500 and 602. In terms of q , what is the value of 1p+1q ?

Answer 1

`(360000q)/(359999)`

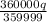
Explanation:

p = Product of all odd integers between 500 an 598. So,

p = 501 x 503 x 505 ... x 595 x 597

q = Product of all odd integers between 500 and 602. So,

q = 501 x 503 x 505 ... x 595 x 597 x 599 x 601

From the above relations, we can see that q is equal to p multiplied by 599 and 601. i.e.

q = p x 599 x 601

or,

`p=(q)/(599 * 601)`

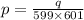
We need to evaluate 1p + 1q in terms of q. Using the value of p from above expression, we get:

`p+q=(q)/(599 * 601) + q\\\\ p+q=(q+(599 * 601q))/(599 * 601)\\ \\ p+q=(q(1+599*601))/(599 * 601)\\\\ p+q=(360000q)/(359999)`