Question

Find the solution of the separable equations a) the general solution: displaystyle dy/dt = t/[y^2] b) the unique solution to: dy/dt = 1/y such that if x = 3 then y = 1.

Answer 1

(a) The general solution of given differential equation is
`(y^3)/(3)=(t^2)/(2)+C`.

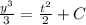(b) The unique solution is
`(y^2)/(2)=t-(5)/(2)`.

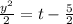Explanation:

(a)

The given differential equation is

`(dy)/(dt)=(t)/(y^2)`

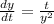
Use variable separable method, to solve the above differential equation.

Separate the variables.

`y^2dy=tdt`

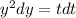
Integrate both sides.

`\int y^2dy=\int tdt`

`(y^3)/(3)=(t^2)/(2)+C`

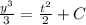
The general solution of given differential equation is
`(y^3)/(3)=(t^2)/(2)+C`.

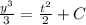(b)

The given differential equation is

`(dy)/(dt)=(1)/(y)`

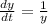
Use variable separable method, to solve the above differential equation.

Separate the variables.

`ydy=1dt`

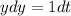
Integrate both sides.

`\int ydy=\int 1dt`

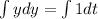
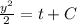`(y^2)/(2)=t+C` ... (1)

It is given that y=1 at t=3. Substitute y=1 and t=3 in the above equation.

`((1)^2)/(2)=(3)+C`

`(1)/(2)-3=C`

`-(5)/(2)=C`

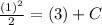
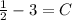
Substitute
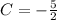`C=-(5)/(2)` in equation (1).

`(y^2)/(2)=t-(5)/(2)`

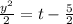
Therefore the unique solution is
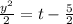`(y^2)/(2)=t-(5)/(2)`.