Answer:
(a) The general solution of given differential equation is
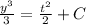 .
.
(b) The unique solution is
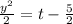 .
.
Explanation:
(a)
The given differential equation is
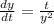
Use variable separable method, to solve the above differential equation.
Separate the variables.
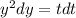
Integrate both sides.
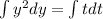
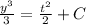
The general solution of given differential equation is
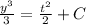 .
.
(b)
The given differential equation is
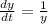
Use variable separable method, to solve the above differential equation.
Separate the variables.
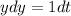
Integrate both sides.
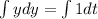
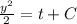 ... (1)
... (1)
It is given that y=1 at t=3. Substitute y=1 and t=3 in the above equation.
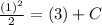
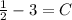
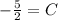
Substitute
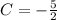 in equation (1).
in equation (1).
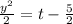
Therefore the unique solution is
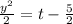 .
.