Question

A store owner claims that the proportion of shoppers who use coupons is less than 25%. To test this claim, a random sample of shoppers are monitored and checked for use of coupons. Assume that the test statistic for this hypothesis test is −1.17. Assume the critical value for this hypothesis test is −1.282. Come to a decision for the hypothesis test and interpret your results with respect to the original claim.

Answer 1

Answer with explanation:

Given : A store owner claims that the proportion of shoppers who use coupons is less than 25%.

Then , the null hypothesis and the alternative hypothesis will be :-

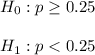`H_0: p\geq0.25\\\\H_1:p<0.25`, since the alternative hypothesis is left tailed , so the test is a left tailed test.

Also,t the test statistic for this hypothesis test is −1.17 and the critical value for this hypothesis test is −1.282 .

We know that when the test statistic value if greater than the critical value , then we reject the null hypothesis.

Here test statistic value(−1.17 ) is greater the critical value(−1.282) for this hypothesis , so we reject the null hypothesis.

So we conclude that there is enough evidence to support the claim.